Bluffstrategier för roulette och varför de inte fungerar
- Varför spelare rent statistiskt förlorar pengar på varje spel de lägger i roulette
- Roulette-strategier som inte fungerar
Roulette är ett av de mest populära casinospelen som finns. Det innebär bland annat att det skrivits spaltmeter om det här spelet på nätet. En del av innehållet är helt legitimt och presenterar saker som de verkligen är. Det finns emellertid en uppsjö av olika webbplatser som försöker vilseleda människor och få dem att spela roulette i tron om att de faktiskt kommer att vinna pengar på lång sikt.
Verkligheten ser tyvärr inte ut så. Det är helt omöjligt att slå ett korrekt fungerande roulettespel över tid, och att konsekvent vinna pengar på ett casino. Oförmågan att slå roulette är djupt inbäddad i spelets grundläggande matematiska och statistiska faktorer. Jag kommer att gå djupare in på det här senare i artikeln.
Fortsätt läsa den här artikeln för att få reda på varför roulette är omöjligt att slå, och varför vanligt förekommande roulette-strategier som utlovar bestående vinster helt enkelt inte fungerar. Jag hoppas kunna förmedla vilka strategier du ska undvika och varför, så att du inte blir lurad av den väldigt frestande, men ofta vilseledande information som kan hittas på nätet.
Jag anser att strategierna i den här artikeln är bedrägliga, eftersom de ofta lovar spelare stora och ihållande vinster. Ett löfte de definitivt inte kan infria. Det finns dock strategier du kan använda för att spela roulette så effektivt som möjligt, och faktiskt maximera dina chanser att lämna casinot med en vinst. Du kan läsa om dem i min artikel om roulette-strategier som fungerar.
Varför spelare rent statistiskt förlorar pengar på varje spel de lägger i roulette
Jag skulle vilja börja med att förklara varför varje insats som placeras på roulettebordet leder till att spelaren långsiktigt förlorar pengar. Som jag redan nämnt ovan, hänger det här ihop med oddsen i roulette, och hur spelet fungerar rent matematiskt.
RTP och husfördel i roulette
Varje casinospel kan karakteriseras av den så kallade återbetalningen till spelare (RTP), vilken beskriver andelen (uttryckt i procent) av varje placerad satsning som statistiskt sett återbetalas till spelare. Om ett spel hade en RTP på 100 %, skulle chanserna att vinna eller förlora vara lika. Casinospel har dock nästan alltid (med några få sällsynta undantag) lägre RTP.
Roulette är inget undantag. RTP för europeisk roulette ligger på 97,3 %, medan RTP för amerikansk roulette är 94,74 %. Det betyder att om en spelare satsar 100 $, vinner han eller hon statistiskt 97,30 $ i europeisk roulette och 94,74 $ i amerikansk roulette. Eftersom dessa vinster är lägre än de ursprungliga satsningarna, är det ganska tydligt att spelaren rent statistiskt förlorar pengar för varje satsning i roulette.
En husfördel är den långsiktiga fördelen casinot har över spelare. Den kan beräknas enligt följande:
Husfördel = 100 % - RTP
Det betyder att europeisk roulette har en husfördel på 2,7 % och att amerikansk roulette har en husfördel på 5,26 %. Detta innebär i sin tur att för varje 100 $ en spelare satsar, så vinner casinot 2,70 $ i europeisk roulette och 5,26 $ i amerikansk roulette på lång sikt.
Läs gärna mer om detta i min artikel om odds i roulette, som även innehåller information om det här spelets RTP och husfördel.
Det du måste veta för att kunna förstå den här artikeln är att det inte finns något sätt att slå roulette, eftersom du statistiskt sett förlorar pengar varje gång du placerar en insats, oavsett vilken typ av insats det rör sig om eller hur mycket pengar du satsar. Det finns ingen väg runt detta faktum.
Roulette-strategier som inte fungerar
Det har äntligen blivit dags att redogöra för de specifika roulette-strategier som faktiskt inte fungerar, men ofta presenteras som felsäkra metoder att tjäna pengar på ett casino.
För var och en av bluffstrategierna listade nedan, kommer jag att inkludera:
- Hur strategin är tänkt att fungera och hur den används
- Varför strategin inte fungerar och varför den kommer leda till att du förlorar dina pengar
- Simuleringar av strategin som används, vilka tydligt visar att det enda möjliga långsiktiga utfallet är att du förlorar dina pengar
Skälet till att dessa strategier är så populära
Många webbplatser presenterar dessa strategier som felsäkra metoder för att tjäna pengar online, då deras enda mål är att få dig att registrera dig på ett onlinecasino via deras länk, vilket gör att de tjänar pengar. De bryr sig inte om det faktum att de ljuger för sina läsare, och bluffstrategierna i den här artikeln kan se väldigt lovande ut vid första anblick, särskilt när de presenteras med vilseledande information.
Det är just därför de förhärligas av ett så stort antal webbplatser, och skälet till att du bör ta informationen om dessa strategier på andra webbplatser med en stor nypa salt.
Martingale-strategin
Den in särklass mest populära bluffstrategin för roulette är Martingale-strategin (även känd som "dubbla upp"-strategin). Det här är också en väldigt enkel strategi, vilket kan ha bidragit till dess popularitet, då i stort sett vem som helst kan använda sig av den utan särskilda förkunskaper.
Martingale-strategin fungerar så här:
- En spelare gör en första satsning, låt oss säga 1 $, på någon av de jämna satsningarna (rött/svart, udda/jämna, hög/låg). Satsningen på rött/svart används oftast, men statistiskt gör det ingen skillnad vilken av satsningarna som väljs.
- Om spelaren vinner, börjar han om och satsar 1 $ igen. Om spelaren förlorar, ska satsningen dubblas. Det här repeteras tills spelaren vinner. Därefter återgår spelaren till att satsa 1 $ igen.
Martingale-strategin fungerar i cykler. Längden på de individuella cyklerna varierar, men var och en av dem bör resultera i att spelaren antingen vinner 1 $ eller förlorar allt. Jag tänker börja med ett vinstscenario och prata om att förlora senare.
Här är några exempel på vinstcykler med tillämpning av Martingale-strategin:
- Spelaren satsar 1 $ och vinner 2 $. Nettovinsten är 1 $.
- Spelaren satsar 1 $ och förlorar. Därefter satsar han 2 $ och vinner 4 $. Spelaren har satsat totalt 3 $ och vunnit 4 $. Nettovinsten är 1 $.
- Spelaren satsar 1 $ och förlorar. Därefter satsar han 2 $, 4 $, 8 $, 16 $, 32 $, 64 $, 128 $, 256 $ och förlorar alla spel. Spelaren satsar sedan 512 $ och vinner. Den totala insatsen landade på 1 023 $ och spelaren vann 1 024 $. Nettovinsten är 1 $.
Alla dessa scenarier slutade framgångsrikt för spelaren, men som du förmodligen redan noterat, var det sista scenariot betydligt värre än de första två. Spelaren förlorade nio satsningar i rad, och vann först på den tionde. Det betyder att spelaren var tvungen att satsa 512 $ bara för att vinna 1 $ under hela cykeln. De snabbt ökande insatserna är ett av de största problemen med Martingale-strategin.
Skälet till att Martingale-strategin ser ut att fungera
Det finns en väldigt fin logiskt förklaring till varför Martingale borde fungera. Om du fortsätter att dubbla din första insats, måste roulettekulan förr eller senare landa på ett nummer som ger dig en vinst. Eller hur?
Ja, det stämmer. När antalet försök närmar sig oändligheten, närmar sig sannolikheten för ett totalt misslyckande noll. Det innebär att du, med obegränsade resurser och i avsaknad av begränsningar satta av casinot, så småningom kommer lyckas att vinna och avsluta en cykel med en nettovinst på 1 $.
Med obegränsade resurser och i avsaknad av begränsningar, skulle hela systemet fungera. Men som du kanske redan förstår, uppfylls aldrig dessa två villkor i verkligheten. Låt oss titta närmare på dessa problem.
Problem 1: Begränsad bankrulle
I verkligheten har varje spelare en begränsad bankrulle. Det betyder att om en spelare fortsätter att använda Martingale-strategin långsiktigt, kommer han eller hon så småningom få slut på pengar, vilket gör det omöjligt att placera en ny insats och avsluta en vinnande cykel.
Låt oss analysera det här med hjälp av ett exempel. Föreställ dig en spelare med en bankrulle på 1 000 $, som använder Martingale-strategin med en första insats på 1 $. Med tillgång till 1 000 $ har spelaren råd att placera följande satsningar efter varandra: 1 $, 2 $, 4 $, 8 $, 16 $, 32 $, 64 $, 128 $ och 256 $. Den totala summan för dessa satsningar uppgår till 511 $, vilket betyder att spelaren efter en förlust av samtliga satsningar bara har 489 $ på sitt konto. Detta gör att spelaren är oförmögen att placera nästa satsning, som borde vara 512 $.
Jag har dock inom ramen för mina beräkningar valt att utelämna detta faktum och betrakta fallet ovan som ett misslyckande. Å andra sidan, i mina simuleringar senare i denna artikel, låter jag de simulerade spelarna fortsätta genom att satsa hela sitt saldo när de saknar tillräckligt med pengar för att följa de insatsstorlekar som dikteras av Martingale-strategin.
Nu kanske du tänker att det är väldigt osannolikt att detta ska inträffa. För att det här scenariot ska realiseras, måste spelaren nämligen förlora 9 satsningar i rad. Vid en första anblick kan det verka som att detta aldrig händer. Men faktum är att det gör det. Och det inträffar oftare än du kanske tror.
Sannolikheten att förlora en jämn satsning 9 gånger i rad på europeisk roulette är:
(19/37)^9 = 0,0025 = 0,25 %
Nej, det är ingen jättesiffra. Denna sannolikhet innebär dock rent statistiskt att 1 av cirka 402 Martingale-cykler kommer att resultera i 9 förlorade satsningar i rad, vilket hindrar spelaren från att lägga ytterligare en satsning.
Självklart har spelaren råd att förlora 9 gånger i rad efter att ha byggt upp sin bankrulle till minst 1 023 $, eftersom det då finns tillräckligt med pengar för att placera den 10:e satsningen på 512 $ efter en förlust av alla föregående satsningar. Efter denna punkt leder endast 1 av cirka 784 cykler till att spelaren blir oförmögen att lägga en ny satsning.
Sannolikheten att förlora en cykel med en tillräckligt stor bankrulle är således ganska låg. Men för att konsekvent vinna pengar med hjälp av Martingale-strategin, måste du upprepa hela processen tusentals gånger, vilket innebär att du förr eller senare förlorar hela din bankrulle. Detta faktum framgår tydligt av simuleringarna av Martingale-strategin som du kan ta del av längre ned i artikeln.
Problem 2: Begränsade insatser
Förutom problemen med bankrullen, är Martingale-strategin även begränsad av de insatsstorlekar som tillåts på det casino du spelar på. Givetvis kan de högsta och lägsta tillåtna bordsinsatserna skilja sig åt mellan olika casinon och spel, men i allmänhet är den högsta tillåtna insatsen ofta bara ett par hundra gånger högre än den lägsta insatsen.
När du spelar på onlinecasinon kan du för det mesta använda flera olika roulettespel med olika bordsgränser för att kringgå dessa begränsningar. Detta är inte särskilt praktiskt, men kan utnyttjas för att minska påverkan från insatsgränser på Martingale-strategins övergripande effektivitet.
Och även om du använder flera roulettebord för att ta dig runt insatsgränserna, är din maximala insatsstorlek fortfarande begränsad. Så även om du hade en oändlig bankrulle (vilket innebär att du inte skulle påverkas av "problem 1" ovan), skulle du ändå vara begränsad av den högsta tillåtna roulettesatsningen du kan hitta.
Problem 3: Inte veta när det är dags att sluta
Som du kanske redan har noterat, är sannolikheten att förlora 9 av 10 satsningar i rad ganska låg. Det är inte särskilt troligt att du ens förlorar 1 av dessa 100 cykler. Faktum är att om du hade en bankrulle som lät dig placera 10 satsningar i rad efter att ha förlorat samtliga tidigare satsningar (från 1 023 $ till 2 046 $) och bara ville vinna 100 $, skulle sannolikheten för att du lyckas vara:
(1-(19/37)^10)^100 = 0,88 = 88 %
Med ett mål att vinna 100 $ skulle sannolikheten att lyckas sålunda ligga på 88 %. I de återstående fallen (12 %) skulle du förlora en stor del av din bankrulle och vara oförmögen att placera ytterligare satsningar.
Med ett vinstmål på 200 $ skulle din chans att uppnå målet vara 77,5 %, med ett vinstmål på 500 $ skulle den vara 52,8 % och med ett vinstmål på 1 000 $ skulle den vara 27,9 %. Som du kan se, minskar sannolikheten att vinna med högre målvinster, vilket givetvis är logiskt.
Problem 3 med Martingale-strategin ligger i det faktum att strategin till en början tycks fungera, vilket får spelare att bli alltför självsäkra och förleder dem att tro att strategin kommer fortsätta att fungera för alltid. Tyvärr gör den inte det. Om en spelare fortsätter att tillämpa Martingale-strategin länge nog, kommer han eller hon förr eller senare att förlora hela sin bankrulle.
Om spelare hade förmåga att identifiera rätt tidpunkt att lämna casinot, skulle flertalet av dem sluta på plus. Det finns dessvärre inte någon optimal tidpunkt att sluta spela på, då det inte finns något sätt att veta när en förlustsvit ska komma. Dessutom finns det inga garantier för att spelare inte kommer förlora allt i Martingale-strategins första cykel.
Simuleringar med Martingale-strategin
Jag har simulerat fem spelare som tillämpat Martingale-strategin medan de spelar europeisk roulette. Här är allt du behöver veta om simuleringarna:
- Varje spelare börjar med en bankrulle på 1 000 $ och grundinsatsen är 1 $.
- Simuleringarna avslutas antingen efter 10 000 rouletteomgångar eller när en spelare förlorar hela sin bankrulle.
- Spelarna följer Martingale-strategin och placerar sina satsningar enligt den.
- Om spelarna inte har tillräckligt med pengar kvar för att placera nästa satsning, satsar de hela sitt återstående saldo. Om de förlorar denna satsning, är de ute ur simuleringen. Om de vinner fortsätter de i enlighet med Martingale-strategin och satsar 1 $ på nästa omgång.
- Jag skapade simuleringarna med hjälp av min egen programvara för simuleringar, vilken använder en RNG (slumptalsgenerator) för att fastställa utfallet av varje omgång. Detta gäller för alla simuleringar i denna artikel. I roulette genereras de slumpmässiga numren av själva roulettehjulet, men resultaten är statistiskt desamma.
Nu tar vi en titt på resultaten:
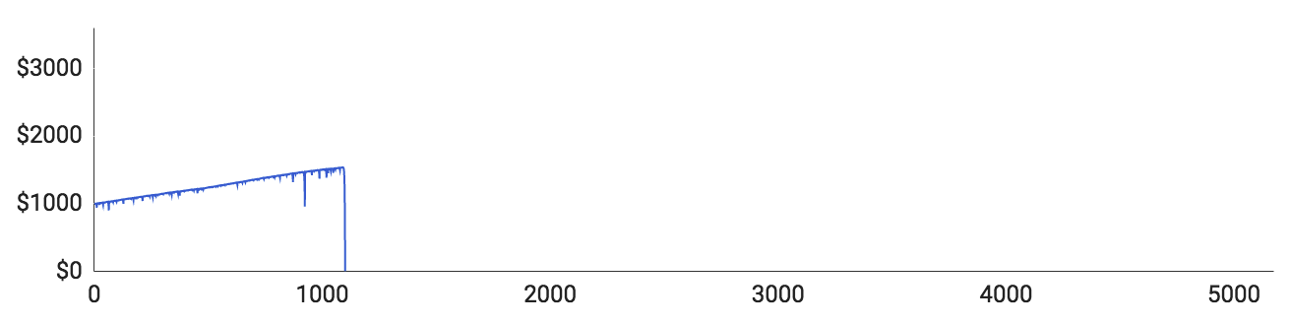
Som du kan se, förlorade samtliga spelare hela sin bankrulle innan de uppnådde 10 000 omgångar. Låt oss kika på de individuella spelare och se efter hur det gick:
- Spelare 1 gjorde inledningsvis ganska bra ifrån sig och lyckades öka sin bankrulle till över 1 500 $, med bara en längre förlustsvit. Spelaren förlorade dock sedan 11 omgångar i rad, vilket tog hans bankrulle från 1 540 $ hela vägen ned till 0 $.
- Spelare 2 hade det värst. Det räckte med 51 omgångar för att han skulle förlora hela sin bankrulle. Detta är ett ganska sällsynt förlopp, men det visar tydligt att saker och ting kan gå utför redan från start.
- Spelare 3 lyckades förlora hela sin bankrulle efter 417 omgångar. Spelaren hade en längre förlustsvit, som han visserligen återhämtade sig från, bara för att drabbas av 11 förlustomgångar i rad kort därefter.
- Spelare 4 förlorade nästan allt under sin 193:e omgång, efter vilken han bara hade 70 $ kvar. Därefter började han sakta bygga upp sin bankrulle igen, men tog sig bara till 477 $. Då hamnade han i en ny förlustsvit som tog honom till 0 $.
- Spelare 5 hade den i särklass bästa spelrundan, men lyckades ändå inte ta hem några pengar. Han lyckades skrapa ihop 3 308 $. Efter det förlorade han 12 omgångar i följd och slutade på noll.
Detta visar att Martingale-strategin verkligen inte fungerar på lång sikt. Samtliga spelare klättrade sakta uppåt, men fick uppleva brutala förlustsviter som resulterade i att de förlorade allt. Detta visar också att de långa förlustsviterna, även om de kan framstå som väldigt osannolika, i själva verket är ganska vanliga.
Fibonacci-strategin
Fibonacci-strategin för roulette är på många sätt lik Martingale-strategin, men det finns några skillnader mellan dem. Jag kommer främst att fokusera på hur dessa två strategier skiljer sig åt.
Först tänkte jag beskriva hur Fibonacci-strategin fungerar. Den är baserad på den berömda sekvensen av s.k. Fibonaccital. Talsekvensen ser ut så här:
1 � 1 � 2 � 3 � 5 � 8 � 13 � 21 � 34 � 55 � 89 � 144 � 233 � 377 � 610 � 987 � �
Du kanske har noterat (eller redan visste) att varje nummer i denna sekvens är summan av de två föregående numren. Den här aspekten av sekvensen används i strategin, även om det kanske inte är märkbart till en början.
Så här används Fibonacci-strategin i roulette:
- Spelaren börjar med att satsa en summa motsvarande det första numret i sekvensen.
- Vid varje förlust flyttar han till nästa nummer i sekvensen och satsar ett motsvarande belopp. Vid varje vinst flyttar han två nummer bakåt. Om spelaren hamnar i början av sekvensen fortsätter han bara att satsa ett belopp som motsvarar det första numret tills han förlorar; därefter fortsätter han enligt strategin.
Den här strategin är inte lika enkel att följa som Martingale-strategin. Nedan följer några exempel som kan hjälpa dig förstå hur den fungerar.
- Spelaren satsar 1 $ och vinner. Cykeln är fullbordad och han startar om från början av sekvensen.
- Spelaren satsar 1 $ och förlorar. Därefter satsar han 1 $ igen (viktigt: den här insatsen motsvarar det andra numret i sekvensen, inte det första) och vinner. Det är meningen att han ska flytta två nummer bakåt, men det finns bara ett nummer (1), så han flyttar dit och satsar 1 $ igen. Om han vinner är cykeln slutförd och han börjar från början igen.
- Spelaren satsar 1 $ och förlorar. Därefter fortsätter han att i följd placera satsningar om 1 $, 2 $, 3 $, 5 $, 8 $, 13 $, 21 $, 34 $ och förlorar samtliga. Sedan satsar han 55 $ och vinner. Det innebär att han återgår till en satsning om 21 $ och fortsätter i enlighet med strategin.
För- och nackdelar med Fibonacci-strategin
Det finns en stor skillnad mellan Martingale- och Fibonacci-strategin. Med Martingale räcker det med en vinnande satsning för att slutföra en vinstcykel. Tillämpningen av Fibonacci-strategin å andra sidan innebär att spelaren slutför en vinstcykel först när han eller hon lyckas flytta sig tillbaka till början av sekvensen och vinner den satsning som motsvarar sekvensens första nummer. Med andra ord, en vinst räcker inte för att ta igen en serie av förluster.
Det betyder att Fibonacci-strategin behöver ett större antal rouletteomgångar för att uppnå samma vinster i jämförelse med Martingale. Det innebär emellertid också att Fibonacci-strategin inte är lika riskfylld.
Simuleringar med Fibonacci-strategin
Simuleringarna av Fibonacci-strategin utfördes på i stort sett samma sätt som simuleringarna av Martingale-strategin. Den enda skillnaden låg i den strategi som de fem simulerade spelarna använde sig av.
Nu tar vi en titt på resultaten:

Graferna nedan påminner om graferna för spelare som använder Martingale-strategin, men det finns några skillnader:
- Graferna stiger i en något lägre takt. Detta överensstämmer med det faktum att Fibonacci-strategin är mindre riskabel och kräver ett större antal spelade omgångar för att uppnå samma vinst.
- Graferna för Fibonacci-strategin varierar mer. Vid tillämpning av Martingale fortsätter de enskilda bankrullarna att öka i ungefär samma takt, tills de sjunker ned till noll. Bankrullarna för spelare som använder Fibonacci-strategin förändras i en mer varierande takt, då en vinnande satsning inte räcker för att bryta en serie av förluster.
Nu ska vi ta en närmare titt på var och en av de fem spelarna:
- Spelare 1 blev den förste att förlora hela sin bankrulle. Det krävdes 488 omgångar för att förlora den och han lyckades inte vid någon punkt ta hem en betydande vinst. Det högsta belopp han uppnådde var 1 074 $. I slutet tog 11 förlorande omgångar honom från 1 067 $ till 0 $.
- Spelare 2 lyckades bättre. Det tog honom 2 291 omgångar att förlora hela sin bankrulle och hans bankrulle var som högst 1 330 $, vilket han uppnådde 27 omgångar innan pengarna tog slut. Av de sista 27 omgångarna vann han bara 4 och förlorade de återstående 23, vilket innebar att hans insatser fortsatte att öka och att han fortsatte att förlorare i en allt snabbare takt.
- Spelare 3 fick spela 4 290 omgångar, men hans bankrulle blev aldrig större än 1 298 $, vilket är lägre än vad spelare 2 hade som mest. Skälet till det är att han nästan förlorade allt tidigare under sin simulering, vilket innebar att han blev tvungen att gå "all-in" med bara 122 $ under sin 656:e omgång. Han lyckades vinna den omgången och började sakta återhämta sig, men drabbades senare av en förlustsvit som ledde till att han förlorade allt.
- Spelare 4 förlorade allt på 1 272 omgångar. Hans bankrulle nådde 1 175 $. Under omgång 1 172 blev han tvungen att gå all-in med 145 $ och lyckades vinna, men förlorade allt under de efterföljande 100 omgångarna.
- Spelare 5 hade mest tur. Han fick spela hela 7 132 omgångar och hans bankrulle klättrade upp till 2 269 $. Dessvärre lyckades han inte ta sig till 10 000 spelade omgångar, då han också fick uppleva en förlustsvit som innebar att han förlorade allt.
Sammantaget påminner Fibonacci-strategin på många sätt om Martingale-strategin, men med skillnaden att allt ökar och minskar i en långsammare takt. Bankrullen ökar långsammare, men insatsstorlekarna ökar också långsammare under förlustsviter. Det är anledningen till att spelarna i simuleringen fick spela ett större antal snurr, samtidigt som deras bankrullar i genomsnitt nådde sina toppar på lägre belopp än vid tillämpning av Martingale-strategin.
D’Alembert-strategin
Både Martingale-strategin och Fibonacci-strategin fungerar genom att öka eller minska det satsade beloppet beroende på utfallet av en enskild omgång. D’Alembert-strategin fungerar på liknande sätt, men skillnaderna i de satsade beloppen är mycket mindre. Det är skälet till att den här strategin är mycket säkrare.
D’Alembert-strategin är också baserad på att spelaren lägger en jämn satsning (rött/svart, jämnt/udda eller högt/lågt). Den fungerar så här:
- Spelaren väljer en första satsning och spelar.
- Varje gång spelaren förlorar, ökar han det satsade beloppet med 1 inför nästa omgång. Varje gång spelaren vinner, minskar han det satsade beloppet med 1 inför nästa omgång.
Låt oss anta att spelaren väljer en första insats om 6 $ och börjar spela. Han satsar 6 $ och förlorar. Han satsar 7 $ och förlorar. Han satsar 8 $ och vinner. Han satsar 7 $ och förlorar. Han satsar 8 $ och vinner. Han satsar 7 $ och vinner. Spelaren har lagt sex spel totalt, varav tre ledde till vinst och tre ledde till förlust. Även om han vann samma antal gånger som han förlorade, ligger han på plus med en vinst på 3 $. Det är exakt så den här strategin fungerar.
När en spelare som tillämpar d’Alembert-strategin vinner samma antal omgångar som han förlorar, kommer han att ligga på plus. Vinsten avgörs av det antal omgångar han vunnit/förlorat. Om han vunnit 10 omgångar och förlorat 10, kommer vinsten att ligga på 10 $ oavsett storleken på den första insatsen.
Det här kanske låter bra, eftersom det verkar riktigt fint att ett lika stort antal vinst- respektive förlustomgångar krävs för att uppnå en vinst. När det gäller jämna satsningar är det dock så att dina chanser att vinna eller förlora inte är 50:50 (trots att namnen på satsningarna antyder det). Faktum är att du statistiskt sett endast kommer att vinna 48,65 % av dina satsningar och förlora resterande 51,35 % i europeisk roulette. Den här diskrepansen är tillräcklig för att göra d’Alembert-strategin olönsam på lång sikt.
För- och nackdelar med d’Alembert-strategin
Fördelen med det här satsningssystemet är det faktum att det är betydligt mindre riskabelt än Martingale och Fibonacci. Strategin är självklart inte riskfri, men eftersom satsningarna ökar långsamt under förlustsviter, behöver du inte en så stor bankrulle. Det är mindre troligt att du förlorar hela din bankrulle och du kommer troligtvis inte ha problem med roulettebordets insatsgränser.
Å andra sidan kan den långsamma ökningen av insatsstorlekar också vara en nackdel. Först och främst kommer du sannolikt inte att vinna särskilt mycket pengar med den här strategin, åtminstone inte när du betänker din första satsning och det antal omgångar du måste spela.
Om du dessutom hamnar i en förlustsvit, lär du upptäcka att det är väldigt svårt att ta sig tillbaka på plus igen. Egentligen behöver du en jämförbar vinstsvit för att lyckas med det. För att jämföra detta med andra strategier, behöver du bara en vinnande omgång med Martingale för att bryta förlustsviten. Med Fibonacci behöver du fler vinstomgångar, men inte lika många som när du tillämpar d’Alembert-strategin.
Simuleringar med d’Alembert-strategin
När jag simulerade d’Alembert-strategin insåg jag att det inte gick att använda 1 $ som första insats, eftersom insatserna ska bli lägre när spelare vinner. Om den första insatsen var 1 $ skulle det inte finnas utrymme för successivt lägre insatser. Samtidigt ville jag inte hamna så mycket högre än 1 $, eftersom jag vill ha något så när jämförbara resultat.
Jag beslutade därför att använda mig av en första insats på 5 $ för denna strategi, och lät spelarna börja med en bankrulle på 1 000 $. Spelarna följde d’Alembert-strategin, och om de nådde en insats på 1 $, fick de fortsätta satsa 1 $ tills de förlorade en omgång och deras insats blev högre.
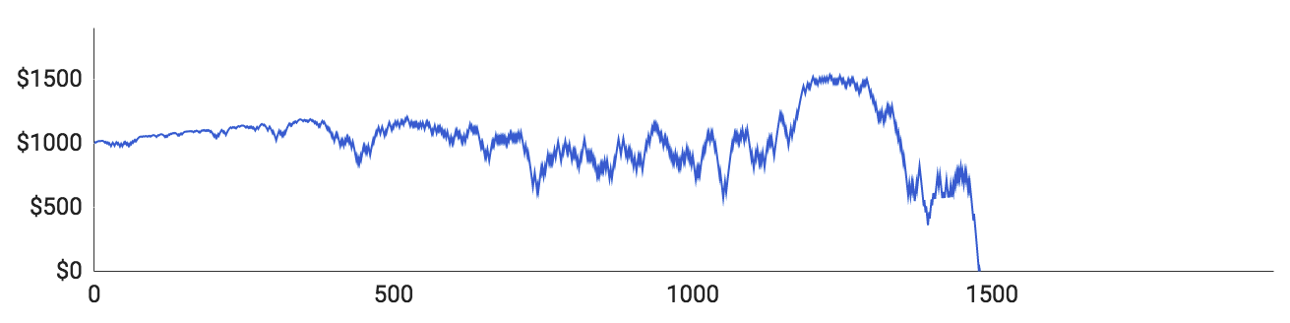
Här är resultaten:
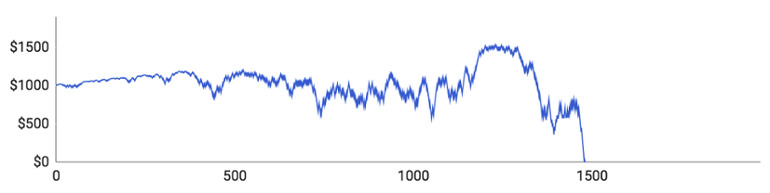
Vi tar en titt på de enskilda spelarna:
- Spelare 1 hann med 1 480 omgångar innan pengarna tog slut. Hans bankrulle toppade på 1 532 $. Hans insatser fortsatte att öka, vilket innebar att upp- och nedgångsfaserna också blev större och större. Det högsta belopp han satsade var 58 $ och den genomsnittliga insatsen för en omgång var cirka 23,40 $.
- Spelare 2 uppnådde bäst resultat. Han spelade totalt 1 971 omgångar och hade vid ett tillfälle en bankrulle på 1 824 $. Han hamnade dessvärre i en längre nedgångsfas som ledde hela vägen ned till 0 $. Spelarens högsta insats landade på 62 $. Den genomsnittliga insatsen var dock bara 16,75 $ eftersom det gick bättre än genomsnittet för just honom. Det är även skälet till att hans insatser generellt förblev ganska små.
- Spelare 3 fick bara spela 406 omgångar och hade verkligen inte turen med sig. Han vann bara på 184 av sina 406 omgångar (45,3 %), vilket är betydligt sämre än den förväntade andelen vinster på 48,65 %. Hans bankrulle toppade på ynka 1056 $.
- Spelare 4 hade inte heller någon vidare tur. Han spelade totalt 563 omgångar och hans bankrulle toppade på 1 172 $. Spelarens snittinsats var 14,70 $ och den högsta insatsen var 50 $.
- Spelare 5 hade en simulering som i allt väsentligt påminner om den för spelare 3. Han spelade bara 517 omgångar och hade aldrig mer än 1 086 $ i sin bankrulle. Av spelarens 517 omgångar slutade bara 236 med vinst (45,7 %).
Du kanske har noterat att jag fäster större uppmärksamhet på insatsstorlekar och den procentuella andelen vinster och förluster för d’Alembert-strategin. Det beror på att denna strategi är tänkt att fungera på så sätt att spelare går plus när de vinner och förlorar lika många omgångar. Det fungerar dessvärre inte så i roulette.
Sammantaget spelade de fem spelarna 4 937 omgångar, varav de vann 2 366 och förlorade 2 571. Det betyder att den totala vinstprocenten bara var 47,9 %. På grund av det större antalet förluster än vinster, fortsatte insatserna generellt att öka. Detta medför också större ned- och uppgångsfaser över tid.
Labouchere-strategin
Labouchere-strategin för roulette är mer komplicerad än de andra strategierna ovan. Den kräver att du håller koll på dina satsningar och adderar ihop siffrorna, vilket kan kräva lite övning.
Labouchere-strategin fungerar så här:
- Spelaren konstruerar en s.k "satsningslinje", som kommer att bestämma storleken på den inledande insatsen, såväl som insatserna för efterföljande spelomgångar, åtminstone till viss del. Det är helt upp till spelaren hur linjen ska se ut. Den kan vara enkel som 1-1-1-1-1-1 eller 1-2-3-4-5-6, eller mer komplex som t.ex. 1-2-4-4-3-7.
- Spelaren tar alltid ett nummer från varje ände av linjen och adderar dem. Summan avgör det belopp som ska satsas under en given omgång.
- Om spelaren förlorar, tar han summan av de två numren han just har satsat och skriver ned den i slutet av linjen. Därefter återgår han till punkt 2 och fortsätter.
- Om spelaren vinner, stryker han båda nummer han tidigare adderat från linjen. Därefter återgår han till punkt 2 och fortsätter.
- Om spelaren får slut på nummer i satsningslinjen, kan ha börja om från början igen, eller skapa en annan satsningslinje.
Jag förstår att det här kan låta lite för komplicerat, så vi ska använda ett exempel för att reda ut allting. Du hittar det i tabellen nedan.
| Omgång | Aktuell satsningslinje | Satsat belopp | Omgångens utfall |
|---|---|---|---|
| 1 | 1-2-3-4-5-6 | 1 + 6 = 7 | FÖRLUST |
| 2 | 1-2-3-4-5-6-7 | 1 + 7 = 8 | VINST |
| 3 | 2-3-4-5-6 | 2 + 6 = 8 | FÖRLUST |
| 4 | 2-3-4-5-6-8 | 2 + 8 = 10 | FÖRLUST |
| 5 | 2-3-4-5-6-8-10 | 2 + 10 = 12 | VINST |
| 6 | 3-4-5-6-8 | 3 + 8 = 11 | VINST |
| 7 | 4-5-6 | 4 + 6 = 10 | ... |
När du använder Labouchere-strategin, är ditt "mål" att bli av med alla nummer i din satsningslinje. Om du lyckas med det kommer din vinst att vara lika med summan av de nummer du började med, oavsett antalet vinster och förluster du fick på vägen dit.
Matematiken fungerar ganska bra med denna strategi, men du måste ha i bakhuvudet att casinot alltid har ett övertag. Labouchere-strategin leder alltså inte till att du på något magiskt sätt slår casinot över tid.
För- och nackdelar med Labouchere-strategin
Labouchere-strategin hamnar någonstans mellan Fibonacci och d’Alembert vad gäller risknivå. Matematiken fungerar verkligen och du hamnar på plus om du lyckas vinna minst lika många omgångar som du förlorar. Men du vet redan att det inte är särskilt troligt att lyckas med det i långa loppet.
Om du drabbas av en förlustsvit, kommer dessutom numren på din satsningslinje att bli högre och högre. Din linje kommer att bli längre och du måste att satsa mer och mer pengar. Och ännu värre är att insatserna kommer att förbli ganska höga även efter att du har börjat vinna. Det kommer att krävas en längre vinstsvit för att få ner dem.
Simuleringar med Labouchere-strategin
Simuleringarna av Labouchere-strategin är ganska komplicerade, eftersom de är avhängiga av listan över nummer som spelaren börjar med. Jag kommer att använda den här satsningslinjen för simuleringarna nedan: 1-2-3-4-5-6.
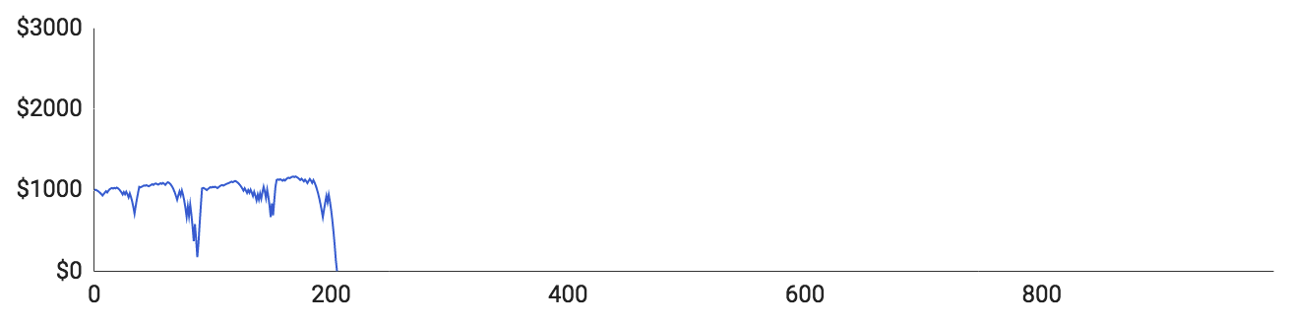
Här är resultaten:
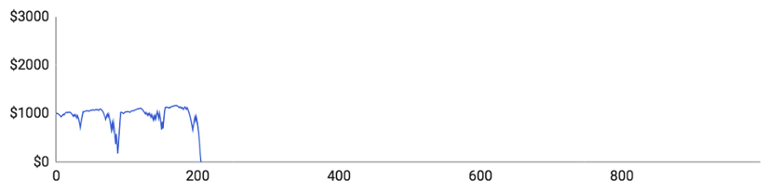
Så här gick det för de enskilda spelarna:
- Spelare 1 fick spela 205 omgångar och hans bankrulle klättrade upp till 1 170 $. Spelarens högsta insats var 240 $ och snittinsatsen landade på 44,65 $. Han upplevde en större förlustsvit som han lyckades återhämta sig från, men förlorade alla pengar efter ytterligare en nedgångsfas.
- Spelare 2 spelade totalt 227 omgångar och nådde en bankrulle på 1 296 € som högst. När det gäller insatser, var hans högsta 272 $ och det genomsnittliga belopp han satsade under en omgång var 28,48 $.
- Spelare 3 fick spela 350 omgångar och hans bankrulle klättrade upp till 1 504 $. Spelarens högsta insats var 377 $ och snittinsatsen landade på 27 $. Hans bankrulle växte ganska stadigt, men en längre nedgångsfas gjorde att han förlorade allting.
- Spelare 4 hade en väldigt intressant spelsession. Han fick spela 996 omgångar, vilket är betydligt fler än någon av de övriga spelarna fick spela. Hans bankrulle toppade på 2 881 $. Detta berodde på att han vann 52,1 % av de omgångar han spelade, vilket betyder att han hade en stor portion tur. Trots hans sanslösa vinstprocent, slutade han ändå på 0 $ efter en tung förlustsvit.
- Spelare 5 fick bara spela 157 omgångar och hans bankrulle toppade på 1 201 $. Hans högsta insats var 205 $ och snittinsatsen landade på 31,57 $.
Resultaten av dessa simuleringar är ganska intressanta, särskilt resultaten för spelare 4, som hade en helt fantastisk session. Simuleringarna pekar tydligt ut de främsta nackdelarna med Labouchere-strategin – de ökande insatsstorlekarna som orsakar stora upp- och nedgångsfaser.
Denna strategi (med den inledande satsningslinjen 1-2-3-4-5-6) tycks vara den mest riskfyllda av de fyra strategierna i denna artikel. Spelarnas bankrullar ökade ganska snabbt, men de lyckades i genomsnitt även förlora allt snabbare. Det här kan givetvis skilja sig väldigt mycket beroende på valet av satsningslinje för simuleringen.
Bättre strategier för roulette
Som du kan se har alla strategier jag analyserat i denna artikel några grundläggande faktorer som gör att det verkar som om de kan fungera, men de kommer förr eller senare leda till att du förlorar hela din bankrulle. Det är därför jag inte rekommenderar att använda dem.
Det finns bättre strategier, som kan maximera dina chanser att lämna casinot med en vinst, eller som åtminstone säkerställer att du har så kul som möjligt medan du spelar. Nu säger jag inte att dessa "bättre strategier" kommer göra det möjligt för dig att vinna långsiktigt, men de är bättre än inga strategier alls. Om du är intresserad, så läs gärna min artikel om roulette-strategier som fungerar.